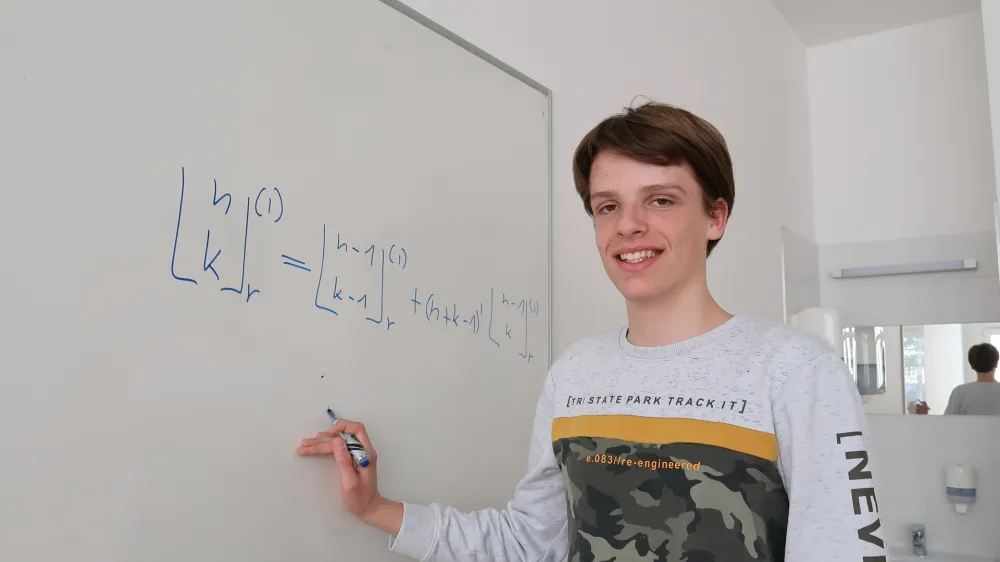»Zadovoljen sem in dobro se počutim, ko vidim, da so v isti številki revije ob mojem objavljeni članki uglednih profesorjev in raziskovalcev,« pravi skromen, a izjemno samostojen in vztrajen mladi matematik, za katerega je bil prelomen šesti razred osnovne šole in – naj se sliši še tako čudno – epidemija in selitev življenja na splet. Med poukom na daljavo je s šolsko snovjo hitro opravil, nato pa si je čas krajšal z raziskovanjem matematičnih učbenikov. Najprej je predelal osnovnošolske, nato naletel na mamin gimnazijski matematični učbenik in ko v njem ni našel nič več novega, se je priključil spletnim predavanjem za študente matematike in doktorskim seminarjem. Prikima, da mu je epidemija pravzaprav prinesla srečo – danes možnosti obiskovanja spletnih predavanj verjetno ne bi več imel, takrat pa se je lahko nanje »pritihotapil« čisto neopazno. Dneve si je zapolnil z urniki spletnih predavanj, medtem ko sta ga mama in oče skušala prepričati, da v življenju obstaja še kaj drugega poleg matematike. Svež zrak, denimo, ali pa prijatelji in zabava.

Ni se pustil kaj prida motiti. Pritegnila ga je kombinatorika. »Bolj ko je težko, bolj zanimivo je,« se posmeje in pove, da kombinatoriko pogosto uvrščajo med najtežje veje matematike, saj združuje veliko matematičnega znanja – od analize, integralov, odvodov do logike. Kombinatorika, pravi, ni samo to, da znamo ženske s kopico parov čevljev, kril in jopic izračunati, na koliko načinov se lahko zjutraj oblečemo, ampak veliko več. »Enumerativna kombinatorika, ena od treh vej kombinatorike, ki je pritegnila mene, je denimo zelo uporabna v genetiki in biologiji. Z njeno pomočjo lahko predvidimo, kolikšna je verjetnost, da se bo rodil potomec s točno določenimi lastnostmi. Na teoriji grafov, drugi veji kombinatorike, temeljijo nekateri navigacijski sistemi. Eden mojih najljubših matematikov Leonhard Euler je denimo na primeru otočka na reki sredi Kaliningrada v Rusiji dokazal pomembno odkritje. Na otok so vodili različni mostovi in meščani so se med preganjanjem dolgčasa zabavali z idejo, kako speljati sklenjeno pot, ki bi vse mostove prečkala zgolj enkrat. Euler je ugotovil, da ni take poti. Vsaj en most oziroma vozlišče je bilo treba prečkati dvakrat. Danes je to dognanje uporabno tudi v računalniških sistemih,« uporabne plati kombinatorike našteje štirinajstletnik. Nasmehne se, da bi s pomočjo kombinatorike lahko izračunali tudi, kako razporediti goste za mizami ob kronanju kralja Karla III., ne da bi se ti med seboj grdo gledali.

Med spremljanjem spletnih predavanj je naletel tudi na eno, ki ga je vodil profesor ljubljanske fakultete za matematiko in fiziko dr. Marko Petkovšek, dober poznavalec kombinatorike. Takrat še sedmošolec se je opogumil in mu napisal elektronsko sporočilo ter mu v isti sapi že poslal dve zanimivi ideji, do katerih se je sam dokopal. »Profesor je bil zadovoljen. Ne zato, ker bi kaj novega odkril, kot sem sprva mislil sam, ampak ker sem se do matematičnih zakonitosti, ki so jih pred mano že odkrili drugi matematiki, dokopal sam, in to peš ter na pravilen način. Za spodbudo mi je poslal knjigo Diskretna matematika 1, v kateri sem se prvič srečal s Stirlingovimi in Lahovimi števili,« pravi. Profesorjeva spodbuda, pohvala in nepodcenjujoč odnos do komaj dvanajstletnika so mladega fanta spodbudili, da je raziskoval naprej.

Nadaljevanje v tiskani izdaji ali mobilni aplikaciji Nedeljskega dnevnika